Những thông tin cơ bản cần biết về bức xạ điện từ ?

1.Khái niệm về bức xạ điện từ :

Bức xạ điện từ (hay sóng điện từ) là sự kết hợp (nhân vector) của dao động điện trường và từ trường vuông góc với nhau, lan truyền trong không gian như sóng. Sóng điện từ cũng bị lượng tử hoá thành những “đợt sóng” có tính chất như các hạt chuyển động gọi là photon.

Khi lan truyền, sóng điện từ mang theo năng lượng, động lượng và thông tin. Sóng điện từ với bước sóng nằm trong khoảng 400 nm và 700 nm có thể được quan sát bằng mắt người và gọi là ánh sáng. Môn vật lý nghiên cứu sóng điện từ là điện động lực học, một chuyên ngành của điện từ học.

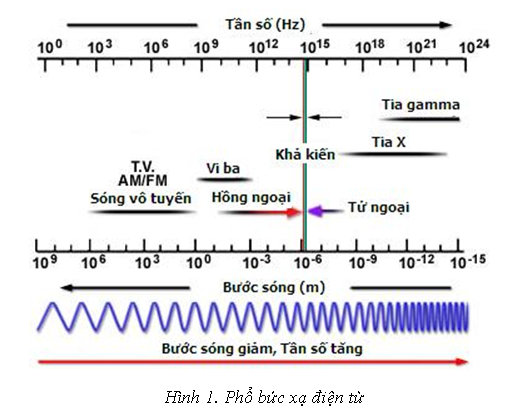
Bức xạ điện từ

2.Phân loại bức xạ điện từ :

Sóng điện từ được phân loại theo bước sóng, từ dài đến ngắn:

Bảng phân chia các bức xạ sóng điện từ/ánh sáng
Tên	Bước sóng	Tần số (Hz)	Năng lượng photon (eV)
Radio	1 mm – 100000 km	300 MHz – 3 Hz	12.4 feV – 1.24 meV
Vi ba	1 mm – 1 met	300 GHz – 300 MHz	1.7 eV – 1.24 meV
Tia hồng ngoại	700 nm – 1 mm	430 THz – 300 GHz	1.24 meV – 1.7 eV
Ánh sáng nhìn thấy	380 nm-700 nm	790 THz – 430 THz	1.7 eV – 3.3 eV
Tia tử ngoại	10 nm – 380 nm	30 PHz – 790 THz	3.3 eV – 124 eV
Tia X	0,01 nm – 10 nm	30 EHz – 30 PHz	124 eV – 124 keV
Tia gamma	≤ 0,01 nm	≥ 30 EHz	124 keV – 300+ GeV

3.Tính chất :

Trong sóng điện từ thì dao động của điện trường và của từ trường tại một điểm luôn luôn đồng pha với nhau.
Sóng điện từ tuân theo các quy luật truyền thẳng, phản xạ, khúc xạ.
Sóng điện từ tuân theo các qui luật giao thoa, nhiễu xạ.
Trong quá trình lan truyền sóng điện từ mang theo năng lượng.

3.1 Vận tốc trong chân không :

Trong chân không, các thí nghiệm đã chứng tỏ các bức xạ điện từ đi với vận tốc không thay đổi, thường được ký hiệu là c=299.792.458 m/s, thậm chí không phụ thuộc vào hệ quy chiếu. Hiện tượng này đã thay đổi nhiều quan điểm về cơ học cổ điển của Isaac Newton và thúc đẩy Albert Einstein tìm ra lý thuyết tương đối.

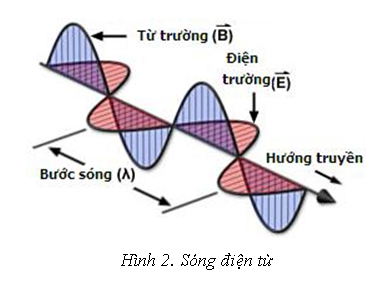
3.2 Sóng ngang :

Sóng điện từ là sóng ngang, nghĩa là nó là sự lan truyền của các dao động liên quan đến tính chất có hướng (cụ thể là cường độ điện trường và cường độ từ trường) của các phần tử mà hướng dao động vuông góc với hướng lan truyền sóng.

3.3 Năng lượng :

Năng lượng của một hạt photon có bước sóng λ là hc/λ, với h là hằng số Planck và c là vận tốc ánh sáng trong chân không. Như vậy, bước sóng càng dài thì năng lượng photon càng nhỏ.

3.4 Tương tác vật chất :

Trong tương tác với các nguyên tử, phân tử và các hạt cơ bản, các tính chất sóng điện từ phụ thuộc ít nhiều vào bước sóng (hay năng lượng của các photon). Dưới đây là một vài ví dụ. Xin xem chi tiết thêm ở các trang dành cho các loại sóng điện từ riêng.

a.Radio :

Radio có ít tương tác với vật chất vì năng lượng của photon nhỏ. Nó có thể đi vượt qua khoảng cách dài mà không mất năng lượng cho tương tác, do vậy được sử dụng để truyền thông tin, như trong kỹ thuật truyền thanh.

Khi thu nạp radio bằng ăng-ten, người ta tận dụng tương tác giữa điện trường của sóng với các vật dẫn điện. Các dòng điện sẽ dao động qua lại trong vật dẫn điện dưới ảnh hưởng của dao động điện trong sóng radio.

b.Vi sóng :

Tần số dao động của vi sóng trùng với tần số cộng hưởng của nhiều phân tử hữu cơ có trong sinh vật và trong thức ăn. Do vậy vi sóng bị hấp thụ mạnh bởi các phân tử hữu cơ và làm chúng nóng lên khi năng lượng sóng được chuyển sang năng lượng nhiệt của các phân tử. Tính chất này được sử dụng để làm lò vi sóng.

c.Ánh sáng :

Các dao động của điện trường trong ánh sáng tác động mạnh đến các tế bào cảm thụ ánh sáng trong mắt người. Có ba loại tế bào cảm thụ ánh sáng trong mắt người, cảm nhận 3 vùng quang phổ khác nhau (tức ba màu sắc khác nhau). Sự kết hợp cùng lúc 3 tín hiệu từ ba loại tế bào này tạo nên những phổ màu sắc phong phú. Để tạo ra hình ảnh màu trên màn hình, người ta cũng sử dụng ba loại đèn phát sáng ở 3 vùng quang phổ nhạy cảm của người.

4. Sóng vô tuyến :

Những sóng điện từ có bước sóng từ vài mét đến vài km được dùng trong thông tin vô tuyến nên gọi là các sóng vô tuyến. Người ta chia sóng vô tuyến thành: sóng cực ngắn, sóng ngắn, sóng trung và sóng dài.

Thang sóng vô tuyến :

Thang sóng vô tuyến

Sự truyền đi của sóng vô tuyến trong khí quyển Trái Đất :

Các loại sóng vô tuyến : sóng dài, sóng trung, sóng cực ngắn bị các phân tử không khí trong khí quyển hấp thụ rất mạnh nên các sóng này không thể truyền đi xa, khoảng cách tối đã của sự truyền sóng này là từ vài km đến vài chục km. Sóng ngắn vô tuyến cũng bị không khí hấp thụ mạnh, tuy nhiên trong một số vùng tương đối hẹp ( tầng điện li ), các sóng ngắn hầu như không bị hấp thụ.

Sóng vô tuyến với ứng dụng chính là dùng trong thông tin liên lạc. Ngoài ra sóng vô tuyến do con người tạo ra có thể dùng cho radar, các hệ thống vệ tinh, mạng máy tính và vô só ứng dụng có ý nghĩa khác.

Năng lượng tần số vô tuyến RF đã được sử dụng trong điều trị y tế hơn 75 năm qua. Sóng vô tuyến được sử dụng để hỗ trợ trong việc phát hiện bệnh và chữa bệnh. Chụp cộng hưởng từ là một ứng dụng hay gặp với việc dùng tần số vô tuyến để tạo ra hình ảnh về cơ thể con người.

5. Lý thuyết :

Lý thuyết điện từ của James Clerk Maxwell đã giải thích sự xuất hiện của sóng điện từ như sau. Mọi điện tích khi thay đổi vận tốc (tăng tốc hay giảm tốc), hoặc mọi từ trường biến đổi, đều là nguồn sinh ra các sóng điện từ. Khi từ trường hay điện trường biến đổi tại một điểm trong không gian, theo hệ phương trình Maxwell, các từ trường hay điện trường ở các điểm xung quanh cũng bị biến đổi theo, và cứ như thế sự biến đổi này lan toả ra xung quanh với vận tốc ánh sáng.

Biểu diễn toán học về từ trường và điện trường sinh ra từ một nguồn biến đổi chứa thêm các phần mô tả về dao động của nguồn, nhưng xảy ra sau một thời gian chậm hơn so với tại nguồn. Đó chính là mô tả toán học của bức xạ điện từ. Tuy trong các phương trình Maxwell, bức xạ điện từ hoàn toàn có tính chất sóng, đặc trưng bởi vận tốc, bước sóng (hoặc tần số), nhưng nó cũng có tính chất hạt, theo thuyết lượng tử, với năng lượng liên hệ với bước sóng như đã trình bày ở mục các tính chất.

Phương trình Maxwell

Có thể chứng minh dao động điện từ lan truyền trong không gian dưới dạng sóng bằng các phương trình Maxwell.

Xét trường hợp điện trường và/hoặc từ trường biến đổi trong chân không và không có dòng điện hay điện tích tự do trong không gian đang xét; 4 phương trình Maxwell rút gọn thành:

$\nabla \cdot \mathbf {E} =0\qquad \qquad \qquad \ \ (1)$

$\nabla \times \mathbf {E} =-{\frac {\partial }{\partial t}}\mathbf {B} \qquad \qquad (2)$

$\nabla \cdot \mathbf {B} =0\qquad \qquad \qquad \ \ (3)$

$\nabla \times \mathbf {B} =\mu _{0}\epsilon _{0}{\frac {\partial }{\partial t}}\mathbf {E} \qquad \ \ \ (4)$

Nghiệm tầm thường của hệ phương trình trên là:

$\mathbf {E} =\mathbf {B} =\mathbf {0}$

Để tìm nghiệm không tầm thường, có thể sử dụng đẳng thức giải tích véc tơ:

$\nabla \times \left(\nabla \times \mathbf {A} \right)=\nabla \left(\nabla \cdot \mathbf {A} \right)-\nabla ^{2}\mathbf {A}$

Bằng cách lấy rôta hai vế của phương trình (2):

$\nabla \times \left(\nabla \times \mathbf {E} \right)=\nabla \times \left(-{\frac {\partial \mathbf {B} }{\partial t}}\right)\qquad \qquad \qquad \quad \ \ \ (5)\,$

Rồi đơn giản hóa vế trái (tận dụng phương trình (1) trong quá trình đơn giản hóa :

$\nabla \times \left(\nabla \times \mathbf {E} \right)=\nabla \left(\nabla \cdot \mathbf {E} \right)-\nabla ^{2}\mathbf {E} =-\nabla ^{2}\mathbf {E} \qquad \quad \ (6)\,$

Và đơn giản hóa vế phải (tận dụng phương trình (4) trong quá trình đơn giản hóa :

$\nabla \times \left(-{\frac {\partial \mathbf {B} }{\partial t}}\right)=-{\frac {\partial }{\partial t}}\left(\nabla \times \mathbf {B} \right)=-\mu _{0}\epsilon _{0}{\frac {\partial ^{2}}{\partial ^{2}t}}\mathbf {E} \qquad (7)$

Cân bằng 2 vế (6) và (7) để thu được phương trình vi phân cho điện trường:

$\nabla ^{2}\mathbf {E} =\mu _{0}\epsilon _{0}{\frac {\partial ^{2}}{\partial t^{2}}}\mathbf {E}$

Có thể thực hiện các biến đổi tương tự như trên để thu được phương trình vi phân với từ trường:

$\nabla ^{2}\mathbf {B} =\mu _{0}\epsilon _{0}{\frac {\partial ^{2}}{\partial t^{2}}}\mathbf {B}$

Hai phương trình vi phân trên chính là các phương trình sóng, dạng tổng quát:

$\nabla ^{2}f={\frac {1}{{c_{0}}^{2}}}{\frac {\partial ^{2}f}{\partial t^{2}}}\,$

với c0 là tốc độ lan truyền của sóng và f miêu tả cường độ dao động của sóng theo thời gian và vị trí trong không gian. Trong trường hợp của các phương trình sóng liên quan đến điện trường và từ trường nêu trên, ta thấy nghiệm của phương trình thể hiện điện trường và từ trường sẽ biến đổi trong không gian và thời gian như những sóng, với tốc độ:

$c_{0}={\frac {1}{\sqrt {\mu _{0}\epsilon _{0}}}}$

Đây chính là tốc độ ánh sáng trong chân không. Nghiệm của phương trình sóng cho điện trường là:

$\mathbf {E} =\mathbf {E} _{0}f\left({\hat {\mathbf {k} }}\cdot \mathbf {x} -c_{0}t\right)$

Với E₀ là một hằng số véc tơ đóng vai trò như biên độ của dao động điện trường, f là hàm khả vi bậc hai bất kỳ, ${\hat {\mathbf {k} }}$ là véc tơ đơn vị theo phương lan truyền của sóng, và x là tọa độ của điểm đang xét. Tuy nghiệm này thỏa mãn phương trình sóng, để thỏa mãn tất cả các phương trình Maxwell, cần có thêm ràng buộc:

$\nabla \cdot \mathbf {E} ={\hat {\mathbf {k} }}\cdot \mathbf {E} _{0}f'\left({\hat {\mathbf {k} }}\cdot \mathbf {x} -c_{0}t\right)=0$

$\mathbf {E} \cdot {\hat {\mathbf {k} }}=0\qquad \qquad \qquad \quad \ \ \ (8)\,$

$\nabla \times \mathbf {E} ={\hat {\mathbf {k} }}\times \mathbf {E} _{0}f'\left({\hat {\mathbf {k} }}\cdot \mathbf {x} -c_{0}t\right)=-{\frac {\partial }{\partial t}}\mathbf {B}$

$\mathbf {B} ={\frac {1}{c_{0}}}{\hat {\mathbf {k} }}\times \mathbf {E} \qquad \qquad \qquad \quad \ \ \ (9)\,$

(8) suy ra điện trường phải luôn vuông góc với hướng lan truyền của sóng và (9) cho thấy từ trường thì vuông góc với cả điện trường và hướng lan truyền; đồng thời E0 = c0 B0. Nghiệm này của phương trình Maxwell chính là sóng điện từ phẳng.